התחדשות עירונית – מודל תחבורה

א. הקדמה

בניה לגובה ותוספת דירות או עיבוי עירוני, הינה תופעה רווחת בערי ישראל ובעיקר באזור המרכז. קיימות סוגיות מהותיות שמשמעותן רווחה ציבורית הנוגעות לצפיפות, חינוך, תשתיות, בריאות ותחבורה. למרות הצורך שבחיזוק מבנים במקרה של רעידות אדמה כדוגמת תמ"א 38, איכות החיים עלולה להנזק מכך. במאמר זה נביא את הסוגיות הרלבנטיות ונציג מודלים כלכליים על מנת לחשב מה המשמעות של אותן משתנים מבחינת איכות החיים של התושבים וערך הנכסים בסופו של דבר. בסופו של דבר, ירידה באיכות חיים משפיעה על התוצר המקומי.

ב. משתנים רלבנטיים

בטבלה הבאה, מובאים מספר משתנים רלבנטיים לבדיקת עיבוי עירוני:

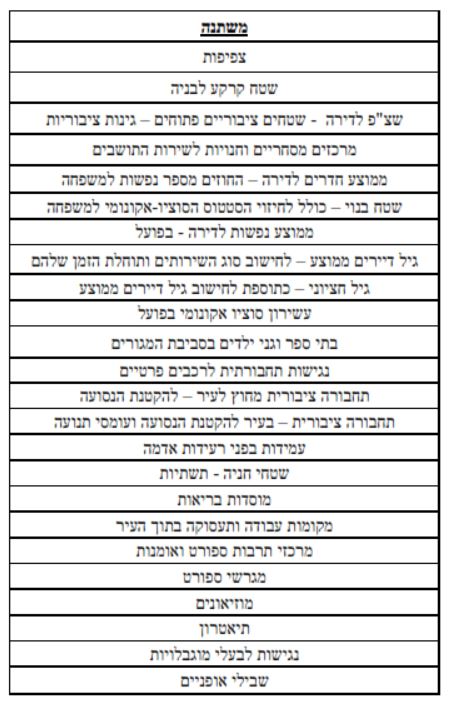
יש לקחת בחשבון את העובדה כי תקציב הרשויות צריך לכסות במידת האפשר שירותים ציבוריים הניתנים לאזרח. הרשויות גובות מיסים מהתושבים וככל שהגביה גבוהה יותר על אותם שירותים שניתנים, כך נחשבת הרשות כחזקה יותר וערך הנכסים בה צפוי לעלות.

ג. מודל כלכלי – תחבורתי

המודל בוחן סוגיות תחבורה באזורים בהם קיימת כוונה לבצע עיבוי עירוני על פי רמת התשתיות. ראשית ברמת העיקרון יש לבחון אם העיבוי נעשה במרכז העיר או בפאתי העיר מאחר ובמרכז העיר בד"כ התנועה והעומסים גדולים יותר וכן קיימת בעיית חניה לרכבים. קיימת חשיבות להיקף התחבורה הציבורית וכושר ההיסע של תושבים ממרכז העיר לפאתי העיר ו/או מחוץ לעיר. המודל שפותח מתייחס לשיעור עומסים בדרך נתונה לפי מאפייניה. המאפיינים הם: תנועת רכבים פרטים וציבוריים, חניה בצידי הדרך, שבילי אופניים, תנועת הולכי רגל, מספר נתיבים לכל כיוון, רמת מינוע שמשמעותה כמות רכבים ליחידת דיור, נסועה במסלול שהוא קילומטרז' ממוצע לשנה למכונית במסלול, כמות רמזורים וצמתים, קצב כניסת מכוניות מצמתים הקשורים למסלול וכדומה. מעריך עומסים ומאפיינים הוא פונקציה של משתנים אלו.

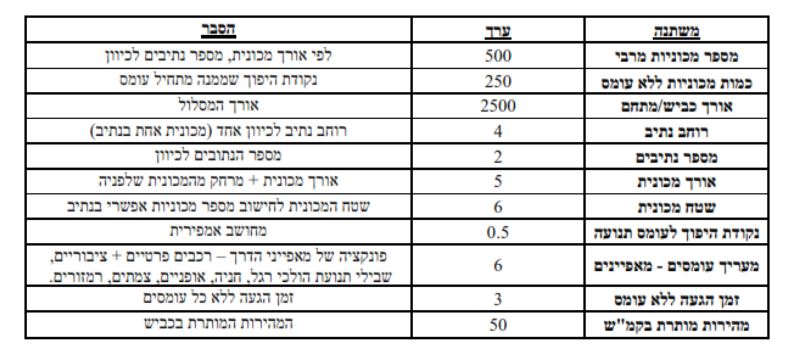
להלן טבלת משתנים בסיסיים לתנועה במסלול שאורכו 2,500 מ"ר:

.
מבחינה אמפירית כשדרך מכילה לפחות 50% מכמות הרכבים המרבים, יורגש עומס אם כי בהתחלה הוא שולי ולאחר מכן משמעותי יותר. להלן מודל חישוב מהירות הנסיעה וזמן ההגעה בהתאם לאורך הדרך הנתון:

יש לציין שברמה התאורטית, במידה והמסלול הוא בשיעור תפוסה של 100% במהירות כניסה ויציאה זהה, לכאורה כל המכוניות ינועו באותו הזמן ובמהירות מותרת ללא כל הפרעה ועיכוב. המודל שפותח מתייחס להתנהגות האנושית כגורם שיוצר עיכובים. הפרעות רבות למהירות התנועה כמו רמזורים, מעברי חציה, אוטובוסים שיוצאים מחניה, קצב כניסת מכוניות מצמתים המתחברים למסלול, מהירות מופחתת כתוצאה מזהירות נדרשת וכדומה גורמים לעומסים בתוך המסלול ולא רק כפונקציה של קצב כניסת מכוניות למסלול וקצב יציאתם מהמסלול. לכן המודל הוא אמפירי ותאורטי כאחד ומשמש כבסיס לבדיקת סוגיות של שירות ציבורי. בכל אופן למהירות כניסה למסלול (קצב כניסת מכוניות) היא מהותית מאחר ומייצרת עומסים בקצב מהיר יותר כאשר מהירות היציאה  קובעת את המהירות הממוצעת המרבית שעל פיה אנו מחשבים את המהירות בעומסים שונים כמתואר בטבלה לעיל. בכל אופן המהירות המרבית במסלול תהיה על פי מהירות היציאה. דוגמה לוויסות מהירות כניסה היא כאשר מצרים נתיבים לפני כניסה לאזור עירוני על מנת להאט את קצב כניסת המכוניות למסלול, רמזורים שמאפשרים הקטנת מהירות ממוצעת לוויסות קצב כניסת מכוניות למסלולים עם עומס גבוה יחסית. כל אלו משפיעים על עומס התנועה מלבד העומס הפנימי בתוך המסלול.  

ד. טבלת ממצאים לזמן ומהירות נסיעה – דוגמה

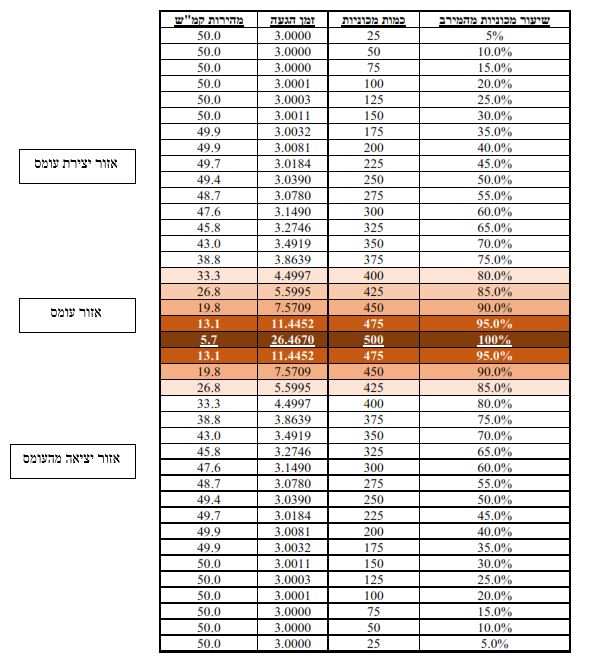
הערה: חשוב להדגיש כי זוהי דוגמה בלבד ועל מנת לחשב את העומס בשעות מסוימות יש להתייחס לכל דרך ומאפייניה על פי הכתוב במאמר זה.

באופן גרפי ניתן לתאר זאת כדלקמן:

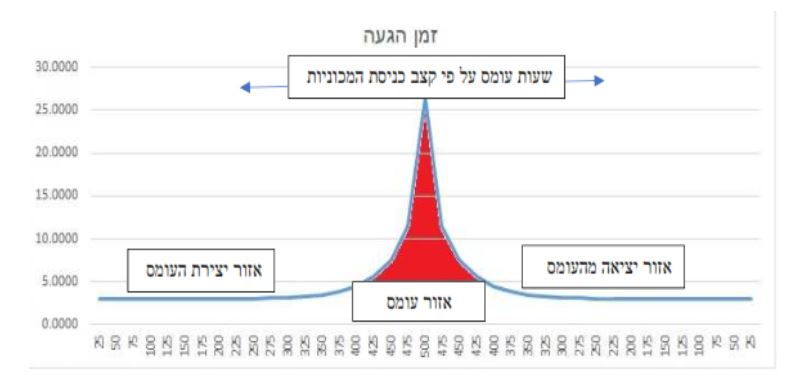
על פי המודל ניתן לחשב את שיעור העיבוי העירוני המרבי במגבלת תשתיות תחבורה, בהינתן מסלולי תחבורה רלבנטיים באזור העיבוי,רמת המינוע בפועל ומאפייני המסלול.

חישוב שעות העומס הוא על פי שעת התחלת העומס והקצב בו מגיעים לשיעור של 100% מכוניות במסלול. במידה וקצב כניסת המכוניות נמוך יותר, כך זמן ההגעה לעומס מרבי יעלה וההפך. קצב כניסת המכוניות הוא פנוקציה של מהירות הנסיעה בכניסה למסלול הנדון. כלומר כאשר העומס מגיע ל – 100% מהירות הנסיעה בדוגמא לעייל היא 5.7 קמ"ש ולכן אין אפשרות להכנס למסלול במהירות הגבוהה ממהירות זו וזה עשוי להשפיע על מסלולים נוספים בסביבת המסלול הנדון. במקרים של קצב כניסה מהיר (מהירות כניסה גבוהה), משך העומס עולה מאחר ומהירות הנסיעה יורדת בקצב מהיר יותר.

לסיכום

פיתוח מודלים מתמטיים ואמפיריים אפשרי לגבי כל שירות ציבורי המוגבל בתקרה. יש להתייחס למודלים הללו כמודלים דינמיים משתנים כפונקציה של עיבוי עירוני. במאמר מוצג מודל תחבורתי גנרי, שניתן ליישמו לגבי כל תחום לרבות: תשתיות – מים, ביוב, חשמל, שירותי בריאות, תרבות וכדומה. השינוי בתפיסה המוצגת לעיל, נובע מהעובדה הבסיסית שככל שמגדילים את העומס הוא אינו גדל באופן ליניארי אלא באופן מעריכי בשל העובדה כי אי הסדר גדל ויוצר אי ודאות הולכת וגדלה בין אם היא נובעת מהתנהגות אנושית ו/או כשלים אקראיים כפונקציה של עומס.

במקרה של מודלים שאינם תחבורתיים, תקופת הבדיקה והמשתנים נקבעים בהתאם לעניין הנדון. לדוגמה – שירותי בריאות – מספר החולים קובע את העומס על חדרי המיון או משך ההמתנה לתורים. במידה ונגדיל את מספר התושבים הנעזרים בשירותי בריאות באזור מסוים, קיימת סבירות למגבלה המוצאת את ביטויה בזמני קביעת התורים ו/או זמן ההמתנה לשירות הרפואי. חשיבות המודל הוא בגמישותו והיכולת להתאימו אמפירית לכל סוג של שירותים ציבוריים הקשורים לעיבוי עירוני ובכלל.